T8.1. Injection d’un soluté dans une veine.

 

1. Equation aux dérivées partielles.

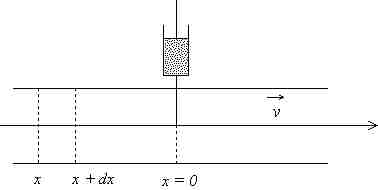
On considère une partie de veine comprise entre les abscisses x et x + dx :

 

La densité molaire de courant due à la diffusion s’écrit :

 

A cette densité molaire de courant, se superpose celle due à l’écoulement que l’on note .

Pendant la durée dt, le volume de soluté qui traverse la section S d’abscisse x est Svdt ce qui représente une quantité de matière cSvdt. Comme  a sa norme qui s’exprime en mol.m^-2.s^-1, l’expression de ce vecteur est :

 

 

La densité molaire totale peut donc alors s’écrire :

 

 

On effectue maintenant un bilan de matière pour la portion de veine comprise entre les abscisses x et

x + dx.

On note dN la variation de la quantité de matière de soluté dans cette partie pendant la durée dt :

 

Or :

             

 

On obtient alors :

 

 

En tenant compte de l’expression de , on obtient finalement :

 

 

2. Cas du régime permanent.

En régime permanent la concentration est constante au cours du temps : .

Comme  c n’est plus une fonction du temps on a l’équation différentielle suivante :

 

 

Par intégration on obtient ;

 

 

Comme pour  on a  et pour x = 0 on a  on obtient :

 

 

Finalement :

 

 

3. Application numérique.

On a alors :

 

avec :