T5.10. Etude d’un cycle
moteur.
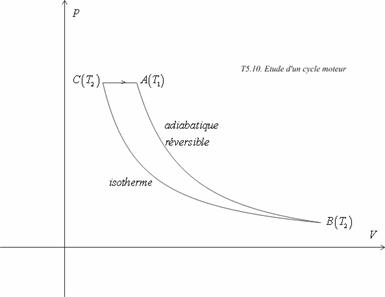
1. Tracé du cycle.
La pente de l’adiabatique
réversible étant « gamma » fois plus grande que
celle de l’isotherme en un point donnée du diagramme
(V, p) cela permet de positionner le
point C à gauche du point A. On
obtient ainsi :
2. Pression initiale.
La loi des gaz parfaits permet
de déterminer la pression initiale
:
3. Température de la source
froide.
La transformation AB est
une adiabatique réversible d’un gaz parfait de
« gamma » constant. On peut alors appliquer la loi
de Laplace.
4. Bilan des quantités de chaleur. Bilan entropique.
Bilan des quantités de chaleur.
●
La transformation AB est adiabatique
donc :
● La
transformation BC est une isotherme. On a
alors :
Avec
volume du gaz au point C. La loi des gaz
parfaits permet d’exprimer ce volume.
● La
transformation CA est isobare.
Bilan entropique.
La
fonction S est une fonction d’état.
Sur
le cycle étudié :
●
Sur l’évolution AB adiabatique et
réversible :
●
Sur l’évolution BC isotherme :
●
Sur l’évolution CA isobare :
On retrouve bien pour un cycle
. L’entropie d’irréversibilité liée à la
transformation CA qui est mécaniquement
réversible mais non thermiquement réversible se
calcule en écrivant :
5. Travail et rendement.
D’après le premier principe
appliqué à un cycle :
Le rendement de ce moteur est :
6. Rendement de Carnot.
Le rendement maximal d’un
moteur thermique ditherme est obtenu avec un moteur
de Carnot dont le cycle est constitué de deux
isothermes et deux adiabatiques réversibles et dont
le rendement de dépend que de la température des
sources.
On a :
car le cycle est irréversible.
