|
T3.6. Transformation polytropique d'un
gaz parfait. 1. Recherche de l'expression
de k.
On applique le premier principe:
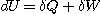
soit :
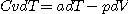 (Eq.A) (Eq.A)
En multipliant par 1/T et en appliquant la
relation d'état du gaz parfait on obtient :
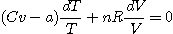
or :
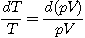
et
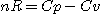 . .
On obtient par intégration :
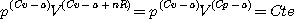
Finalement :
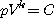
avec C une constante et
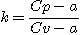
2. Etude des cas
particuliers.
On peut exprimer a en fonction de k :
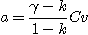 (Eq.B) (Eq.B)
- Pour a
= Cv (Eq.A) s'écrit -pdV =0. La
transformation est isochore. (Eq.B) implique alors
que
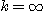 . .
- Pour a
= Cv (Eq.B) implique que k = 0. La
transformation est isochore.
- Pour a
= 0, on retrouve la loi de Laplace
caractéristique d'une transformation adiabatique
réversible dans le cas d'un gaz parfait de
g
constant.
- Pour 1/a
= 0 on obtient k = 1. On retrouve la loi de
Mariotte, la transformation est isotherme.
|