M9.22. Pendule à point d’attache mobile.

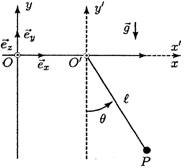
On désigne par R’(O'x'y'z') un repère d'origine O' dont les axes orthogonaux O'x', O'y' et O'z' sont respectivement parallèles aux axes Oy et Oz d'un repère R(Oxyz) que l'on supposera galiléen.

Un pendule simple est constitué d'un point matériel P de masse m, suspendu à l'origine O' de R’ par un fil sans masse ni raideur et de longueur l. On note  l'angle que fait le fil, que l'on supposera constamment tendu, avec la verticale Oy de R (cf. figure ci-dessous).

 

 

 

 

1. Dans un premier temps, l'origine O' de R’ reste fixe et confondue avec l'origine O de R. Quelle doit être la longueur l du fil pour que la période des petits mouvements du pendule soit To = 1 s. On prendra pour norme de l'accélération de la pesanteur la valeur g = 9,8 m/s².
2. Le repère R’ est maintenant animé d'un mouvement de translation rectiligne uniformément accéléré d'accélération constante
   
    avec a > 0.
   Calculer, dans le référentiel R’, par rapport au point O’, le moment des différentes forces appliquées au point P.
3. Déduire du théorème du moment cinétique appliqué en O' dans R’ au point matériel P l'équation différentielle à laquelle obéit l’angle
   
   .
4. Déterminer la valeur
   
    de l'angle
   
    correspondant à la position d'équilibre du pendule.
5. Exprimer la période T des petits mouvements autour de la position d'équilibre
   
    en fonction de l, a et g.