M9.13. Energie cinétique d'une masse sur un axe en rotation.

1. Energie cinétique en Mo'.

On se place dans le référentiel tournant R(O, X, Y, Z)  et on y étudie le mouvement du point M soumis à son poids, la réaction de la tige, les forces d'inertie d'entraînement et de Coriolis.

On applique dans ce référentiel le théorème de l'énergie cinétique entre les points Mo et Mo'.

Dans ce référentiel R seule la force d'inertie d'entraînement travaille ( le travail de celui de  la force de Coriolis étant toujours nul ). On a donc :

Dans R, la vitesse initiale du point M en Mo.

Comme le point coïncident à M est animé d'un mouvement circulaire uniforme dans Ro on a :

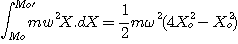
On obtient finalement pour l'énergie cinétique en Mo' :

2. Travail de la réaction dans Ro.

On applique dans Ro le théorème de l'énergie cinétique. Dans ce référentiel, galiléen, la masse m est soumise à son poids et à la réaction du support.

Dans ce référentiel la réaction n'est pas normale au vecteur déplacement ( elle est contenue dans un plan perpendiculaire à la tige OX et sa direction n'est pas parallèle à celle de OZ ). Le travail de la réaction n'est donc pas nul. Par contre le travail du poids est nul car cette force est contenue dans un plan perpendiculaire à la tige OX et sa direction est parallèle à celle de OZ. D'où :

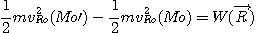
Or d'une manière générale en appliquant la composition des mouvements :

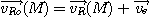
Comme le point coïncident à M est animé d'un mouvement circulaire uniforme de rayon X dans Ro on a :

et pour la vitesse en Mo et en Mo' dans Ro :

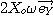
D'où :

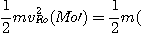
car 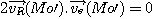 ces deux vecteurs étant orthogonaux

Le travail de la réaction de la tige s'écrit :

Le travail d'une force dépend du référentiel d'étude.