M9.12. Mouvement d'un anneau sur un cerceau en rotation (II).

 

1. Equation différentielle.

On étudie l'anneau A dans le référentiel Rc lié au cerceau.

Ce système est soumis à :

• son poids qui dérive d'une énergie potentielle de pesanteur Ep_p qui a pour expression :
  
  
  
   
   
  En prenant la référence de cette énergie potentielle dans le plan Ox'y', on obtient :
   
• à la réaction du cerceau qui ne travaille pas dans Rc car elle est, dans ce référentiel, toujours normale au déplacement de l'anneau du fait de l'abscence de frottements.
• à la force d'inertie de Coriolis dont le travail est toujours nul.
• à la force d'inertie d'entraînement qui dérive d'une énergie potentielle Ep que l'on détermine. Comme le mouvement d'entraînement est un mouvement de rotatation uniforme autour de l'axe Oz', on a :
   
  avec H projeté de A sur l'axe Oz'.

 

On choisit pour référence de l'énergie potentielle "centrifuge" la position de A pour la quelle l'angle polaire est nul. D'où :

Comme le mouvement de l'anneau dans Rc est circulaire de centre C  et de rayon  R  son énergie cinétique est :

 

L'énergie mécanique de M se conserve dans Rc et vaut :

 

En dérivant cette expression par rapport au temps on obtient l'équation différentielle vérifiée par l'angle polaire :

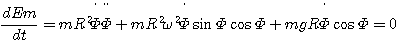
 2. Positions d'équilibre.

L'énergie potentielle U du point matériel dans Rc s'écrit :

 

En dérivant par rapport à l'angle polaire :

Les positions d'équilibre correspondent aux extremums de la fonction U. Soit :

La stabilité des positions d'équilibre est liée au signe de la dérivée seconde de l'énergie potentielle U par rapport à l'angle polaire :

Pour :

• 
  Cette position est une position d'équilibre instable et cela quelque soit la vitesse angulaire.

• 
  La stabilité de cette position dépend de la vitesse angulaire.
  Pour :
  stable
  instable
•     
  Pour :
  stable

En conclusion, suivant la valeur de la vitesse angulaire du cerceau, on a :

• 
    instable
  instable
     stable.

• 
    instable
  stable