M9.11. Mouvement d'un anneau sur un cerceau en rotation.

1. Equation différentielle.

On étudie l'anneau M dans le référentiel Rc lié au cerceau.

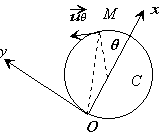
Ce système est soumis à :

son poids qui ne travaille pas lors d'un déplacement horizontal

à la réaction du cerceau qui ne travaille pas dans Rc car elle est, dans ce référentiel, toujours normale au déplacement de l'anneau du fait de l'absence de frottements.

à la force d'inertie de Coriolis dont le travail est toujours nul.

à la force d'inertie d'entraînement qui dérive d'une énergie potentielle Ep que l'on détermine. Comme le mouvement d'entraînement est un mouvement de rotation uniforme autour de l'axe Oz, on a :

 

 

 

 

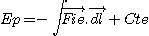
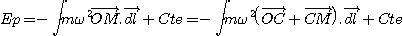
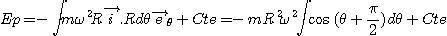
On choisit pour référence de l'énergie potentielle "centrifuge" la position de M pour la quelle l'angle polaire est nul. D'où :

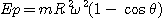
Comme le mouvement de l'anneau dans Rc est circulaire de centre C  et de rayon  R  son énergie cinétique est :

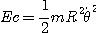
L'énergie mécanique de M se conserve dans Rc et vaut :

 

En dérivant cette expression par rapport au temps on obtient l'équation différentielle vérifiée par l'angle polaire :

 

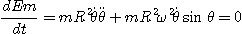
2. Positions d'équilibre.

On étudie la fonction énergie potentielle.

Sa dérivée première :

 

s’annule pour  et  qui constituent des positions d’équilibre.

Le signe de la dérivée seconde de l’énergie potentielle permet de statuer sur la stabilité ou l’instabilité de ces positions d’équilibre :