M8.4. Rotation d’une roue autour d’un axe fixe.

1. Condition de roulement sans glissement.

Soit I le point appartenant à la roue et en contact avec le sol. S'il n'y a pas de glissement la vitesse de ce point par rapport au référentiel  lié au sol est nulle.

On exprime cette vitesse en faisant intervenir le référentiel  lié à la tige OO1 et en rotation uniforme autour de l'axe Oz :

 

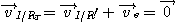
La vitesse d'entraînement est la vitesse d'un point fixe I' de  coïncident avec le point I à la date t et que l'on évalue dans le référentiel . Le point I' décrit un cercle de rayon R à la vitesse angulaire ω. La vitesse d'entraînement a donc pour expression :

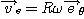
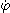Dans le référentiel  le point I décrit un cercle de rayon a à la vitesse angulaire. Soit :

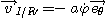
La condition de roulement sans glissement  est donc :

 

2. Vitesse et accélération de M par rapport au sol.

On utilise pour déterminer ces deux grandeurs les formules de composition :

Pour la vitesse.

 

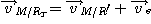
La vitesse d'entraînement du point M est identique à celle du point I.

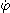Dans le référentiel  le point M décrit un cercle de rayon a à la vitesse angulaire. Soit :

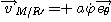
En écrivant la condition de roulement sans glissement on obtient :

Pour l'accélération.

L'accélération d'entraînement est l'accélération d'un point fixe de  coïncident avec le point M à la date t et que l'on évalue dans le référentiel  Le point coïncident décrit un cercle de rayon R à la vitesse angulaire ω. L'accélération d'entraînement à donc pour expression :

 

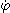Dans le référentiel  le point M décrit un cercle de rayon a à la vitesse angulaire. Soit :

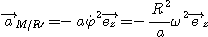
Pour l'accélération de Coriolis, en utilisant la condition de roulement sans glissement ::

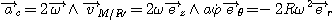
On obtient pour expression de l'accélération :

 

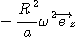
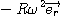
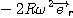
On obtient pour la norme de ces vecteurs :