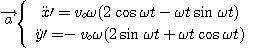M8.1. Etude du mouvement d'une balle dans un référentiel tournant.
1. Coordonnées.
La trajectoire de la balle M est contenue dans le plan horizontal z =
0. On a :

On exprime les vecteurs
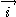 et
et
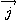 en
fonction des vecteurs
en
fonction des vecteurs
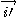 et
et
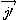 .
.

En remplaçant et par identification, on détermine :
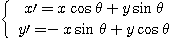
2. Trajectoire.
Dans le référentiel lié au sol on a :
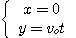 le
mouvement étant rectiligne uniforme.
le
mouvement étant rectiligne uniforme.
Le mouvement de la balle, par rapport au référentiel lié au plateau et de
repère (O,x', y') s'écrit :
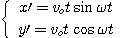
En établissant un tableau de valeur pour x', y' pour
différentes valeurs de
ωt, et en traçant
y' =f(x' ), on montre que la trajectoire est une spirale.
3. Vitesse et accélération.
Dans le référentiel lié au plateau :
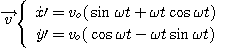
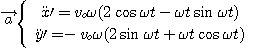
4. Lois de composition.
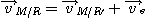
Le point fixe de R' qui coïncide avec le point système M étudié est
animé d'un mouvement circulaire uniforme par rapport au référentiel R.
La vitesse d'entraînement s'écrit alors dans la base de R' :
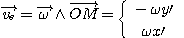
La loi de composition exprimée dans la base de R' s'écrit :
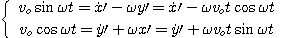
D'où :
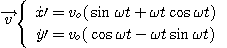
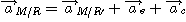
L'accélération du point M dans R est nulle car le mouvement y est
rectiligne uniforme.
Le point coïncident est animé d'un mouvement circulaire et uniforme dans
R , d'où :
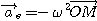
L'accélération de Coriolis a pour expression :
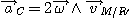
En exprimant la loi de composition dans la base de R', on obtient :
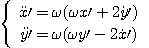
On obtient finalement :