M7.2. Mouvement
hyperbolique d’un satellite artificiel.
Un satellite artificiel
A, de masse m = 2000 kg, est placé sur une orbite circulaire
d'attente, de rayon ro = R + h
autour de la Terre
(h = 180 km, R = 6400 km rayon de la
Terre). Lorsque le satellite atteint un point M de cette trajectoire,
on lui communique un excédent de vitesse. La nouvelle vitesse v1
est tangente à l'orbite circulaire et vaut 14 km/s.
- Exprimer en fonction
de ro, G (constante de la
gravitation) et MT (masse
de la Terre) la valeur vo
de la vitesse lorsque le satellite est sur son orbite d'attente.
Calculer numériquement vo
ainsi que son énergie mécanique.
- Montrer que la
nouvelle trajectoire est contenue dans un plan que l'on déterminera et
calculer la nouvelle valeur de l'énergie.
- Etablir que l'équation
de la trajectoire s’écrit dans ce plan :
e et p étant deux constantes dont on donnera la
signification, r la coordonnée radiale et
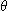l'angle
que fait le rayon vecteur avec le rayon vecteur initial.
- Exprimer p en
fonction du moment cinétique et calculer sa valeur. En déduire
e.
Données :
MT =
6,02.1024 kg
G = 6,67.10-11 S.I
