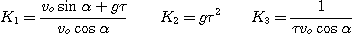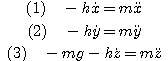On travaille dans le
référentiel terrestre supposé
galiléen. On considère le point M
de masse m. Les forces
appliquées à ce système sont :
On applique la
relation de la dynamique :
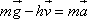
On projette cette
relation dans la base du référentiel
d'étude :
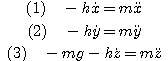
On pose :
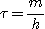
Pour l'équation
(1) :
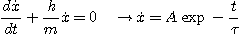
En tenant compte des
conditions initiales suivant Ox :
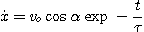
Une seconde
intégration conduit à :
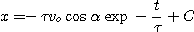
Comme à t =
0, x(t=0) = 0 on a:
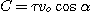
D'où:
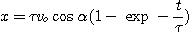
Pour l'équation
(2):
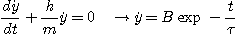
Comme à t = 0
la composante de la vitesse suivant
Oy est nulle, on a B = 0.
Une seconde
intégration conduit, compte tenu du
fait que l'objet part de la position
O à t = 0, à
y = 0.
Le mouvement du
système est donc contenu dans le
plan Ox, Oy.
Pour l'équation
(3) :
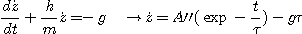
A t = 0, on a
:
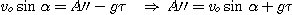
La composante de la
vitesse suivant Oz a pour expression
:
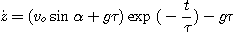
Une seconde
intégration conduit à :
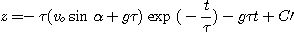
Comme l'objet part
de O à la date du lancement, on a à
la date t = 0 :
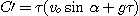
On obtient pour la
composante z :
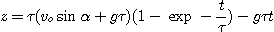
L'équation horaire
x(t) permet d'écrire :
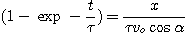
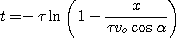
En substituant dans
l'équation z(t), on obtient :
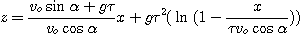
Par identification
avec la forme demandée on a :