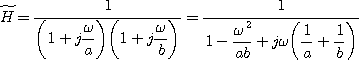E5.4. Biporte RC du second ordre.

1. Fonction de transfert.

Soit A le point de connexion des deux résistances et du condensateur C1.

L'association série R2, C2 réalise un pont diviseur de tension. On a donc :

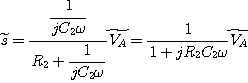
On applique le théorème de Millman au point de connexion A des deux résistances et du condensateur C1:

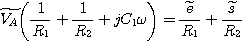
En remplaçant l'expression de 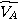ainsi déterminée dans la première équation on obtient la fonction de transfert :

 

 

2. Autre forme de la fonction de transfert.

On écrit la fonction de transfert sous une forme plus symétrique :

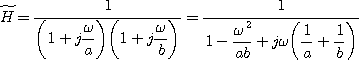
Par identification avec le résultat de la première question, on obtient :

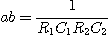     et       

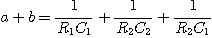
Les coefficients a et b, dont on connaît la somme S et le produit P sont solution de l'équation du second degré :

 

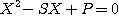
3. Etude de la réponse en gain.

La fonction de transfert s'écrit :

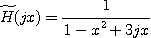
Le gain exprimé en dB a pour expression :

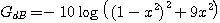
La fonction 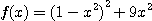est strictement croissante. Il s'ensuit que le gain maximum est nul et est obtenu pour x =0.

La bande passante est définie par l'ensemble des pulsations réduites vérifiant :

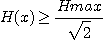 ici Hmax = 1 d'où les limites de la bande passante sont données par :

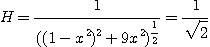
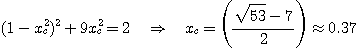
On obtient finalement pour la pulsation de coupure :

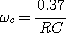
On peut remarquer que la pulsation de coupure est différente de .

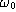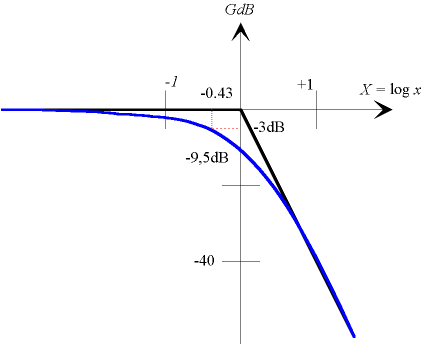
La courbe de réponse en gain admet :

• en basse fréquence :
  une asymptote horizontale à GBF = 0 dB
• en haute fréquence :
  une asymptote passant par l'origine de pente - 40 dB/ décade
  GHF = -40 log x = -40 X
• pour x = 1, GdB = -9,5 dB

 

La courbe de réponse en gain ets alors :