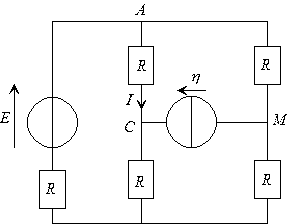
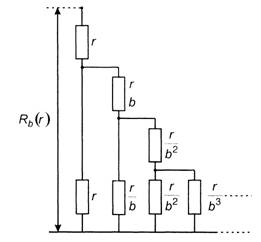
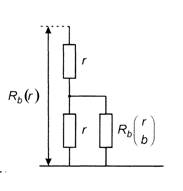
|
électricité \ électromagnétisme \ électronique \ mécanique \ optique \ thermodynamique |
|
|
||
|
||
|
www.kholaweb.com \ h de haan \ mise à jour :
25 juin 2011 |
||