T6.5. Machine à vapeur.
On adopte le modèle de machine
à vapeur suivant : un système fermé constitué d'un
kg d'eau sous deux phases liquide et vapeur décrit
un cycle ABCD. Les évolutions BC et
DA sont adiabatiques et réversibles; les
évolutions AB et CD sont
isothermes-isobares. On note x le titre
massique en vapeur. Les données concernant le
cycle sont résumées dans le tableau ci-après.
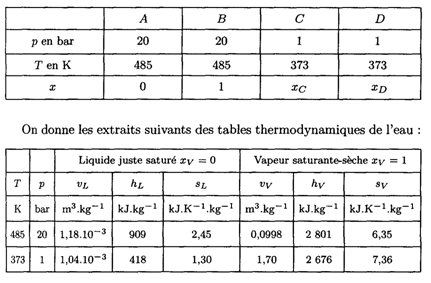
1.
Donner l'allure du cycle dans un diagramme de
Clapeyron. Faire aussi figurer la courbe de
saturation.
2.
Calculer les titres en vapeur xC et xD, les volumes massiques vC et
vD, les enthalpies massiques hC et
hD et les énergies internes massiques uC,
uD,
uA,
uB.
3.
Calculer les travaux et les transferts
thermiques reçus par l'eau au cours de chacune des
évolutions AB, BC, CD et DA.
4.
Définir le rendement thermodynamique r
de cette machine et le calculer.
Comparer r
au rendement d’un moteur de Carnot
fonctionnant entre des sources à Tc = 485 K
et Tf = 373 K ; commenter le résultat.
T6.5. Machine à vapeur.
1. Allure du cycle.
Le point A est placé sur
la courbe d’ébullition car le titre en vapeur en ce
point est nul et la pression est égale à la pression
de vapeur saturante à cette température. Le point
B est lui situé sur la courbe de rosée car le
titre en vapeur est égal à 1 et que la pression pour
ce point est la pression de vapeur saturante à cette
température.
2. Caractéristiques des
différents états.
● La transformation DA
est isentropique, on peut alors écrire que :
De la même manière on obtient
en utilisant le caractère isentropique de la
transformation BC le titre en vapeur
au point C :
● Le volume massique est défini
en un point de la transformation par :
Au point C :
De la même manière, on obtient
au point D :
● Pour l’enthalpie massique, on
suit le même type de définition que pour le volume
massique.
On obtient ainsi pour le point C :
De même :
● L’énergie interne massique
est définie par : u =h-pv. On obtient :
3. Bilan énergétique.
● Pour la transformation
AB isobare isotherme:
Sur une transformation isobare,
la quantité de chaleur échangée par le système avec
l’extérieur est égal à la variation d’enthalpie du
système. Soit :
● Pour la transformation
BC adiabatique et réversible :
● Pour la transformation
CD isobare isotherme :
● Pour la transformation
DA adiabatique et réversible :
Le travail total massique
échangé par cette machine est :
Comme w < 0 la machine
étudié est bien un moteur.
4. Rendement.
Le rendement r de cette
machine est défini par le quotient du rapport entre
la grandeur valorisable (ici la valeur absolue du
travail w total échangé avec le monde
extérieur) et la grandeur coûteuse (
énergie nécessaire pour effectuer la transition de
phase entre les états A et B).
Le rendement de Carnot
s’exprime en fonction de la température des sources
par :
Le moteur étudié décrivant un
cycle de Carnot (deux isothermes, deux adiabatiques
réversibles) il est donc normal de trouver son
rendement égal à celui de Carnot.
Il est à noter que ce rendement
maximal d’un moteur est indépendant de la nature du
fluide utilisé.
