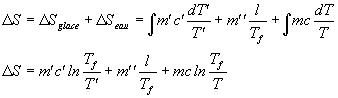
1. Composition du mélange à l'état final.

Différents cas peuvent se présenter pour l'état final à la pression atmosphèrique :

Totalité du mélange sous forme de glace à une température inférieure à O°C

Totalité du mélange sous forme de glace à une température égale à O°C

Mélange eau-glace à 0°C

Totalité du mélange sous forme d'eau à une température inférieure à O°C

Totalité du mélange sous forme d'eau à une température supérieure à O°C

Pour choisir entre ces différentes possibilités on regarde si le glaçon peut "fondre" en totalité et se retrouver sous forme d'eau liquide à 0°C. Soit Q₁ l'énergie nécessaire pour réaliser cette transformation.

Q₁ = - m'c'T '+m'l

Cette énergie est fournie par l'eau liquide :

Q₂ = -mcT

On calcule le rapport Q₁/Q₂. La valeur de ce rapport, inférieure à 1, indique que l'eau liquide ne peut entraîner la fusion complète du glaçon.

Ce calcul élimine donc les deux derniers cas.

On fait maintenant l'hypothèse d'un mélange eau-glace à 0°C et soit m'' la masse de glace prise à 0°C et ayant subi la fusion.

Le bilan enthalpique sur le système eau-glace ( dans cet exercice on ne tient pas compte du comportement du calorimètre) donne :

DH = 0 = m'c'(0 - T ' ) + m''l + mc(0 -T)

On détermine ainsi m'' = 0,225 kg. Ce résultat étant inférieure à m', valide l'hypothèse posée.

Le mélange, dans l'état final à la température de 0°C est constitué de 175 g de glace et de 1,225 kg d'eau liquide.

2. Variation d'entropie.

L'entropie étant une grandeur extensive et une fonction d'état, on détermine la variation d'entropie du système en calculant la variation d'entropie pour chaque partie du système et en considérant la transformation réversible. En posant T_f = 0°C, on obtient :

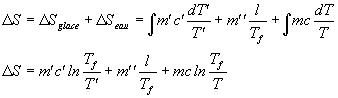
En prenant bien soin d'exprimer les températures en degrés kelvin :

DS = 10,3 J/K