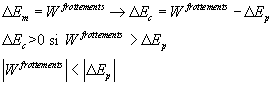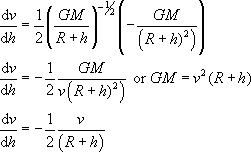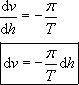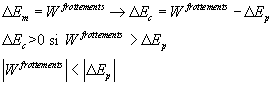M7.4. Freinage d’un satellite.

On travaille dans le référentiel géocentrique, de centre O, supposé galiléen (la masse m du satellite étant négligeable devant celle de la Terre de masse M).

Le satellite S est soumis à la force de gravitation :

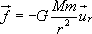
Dans le cas d’un mouvement circulaire, le vecteur vitesse est toujours orthogonal au vecteur position. La force de gravitation a donc, dans cette configuration, une puissance nulle. Le mouvement du satellite est circulaire uniforme.

On écrit le principe de la dynamique dans la base cylindro-polaire sachant que le mouvement est circulaire et uniforme :

 

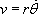
La vitesse du satellite a pour expression :

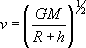
La variation de la vitesse en fonction de l’altitude h est exprimée par :

           

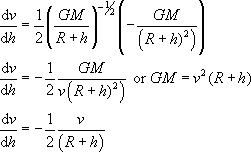
Le mouvement étant quasi circulaire uniforme, on peut exprimer la vitesse en fonction de la période de révolution T :

 

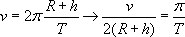
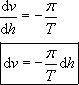
Comme dh < 0 on a dv > 0. Sous l’effet des forces de frottement la vitesse du satellite augmente !

L’accroissement de l’énergie cinétique vient du fait qu’en valeur absolue, l’énergie dissipée est plus faible que la diminution de l’énergie potentielle de pesanteur. En effet :