M10.5. Pendule de Foucault.
Enoncé.
On
considère un pendule simple constitué d'une
masselotte A de masse m = 30 kg
suspendue à l’extrémité
inférieure d'un filin de longueur l = 67 m.
L'autre extrémité est fixée en un point O1
à une hauteur égale à l sur la
verticale du lieu de latitude
λ.
-
Déterminer l'équation vectorielle du mouvement.
On notera la tension sous la forme
.
-
Expliciter les équations différentielles du
mouvement dans la base du référentiel terrestre
(R) locale
, Oz
étant la verticale ascendante et Ox l'axe
local orienté vers l'est.
On notera :
Ω la
vitesse de rotation de la Terre autour de l'axe
des pôles,
θ la
colatitude,
.
En déduire que les équations différentielles du
mouvement dans le plan horizontal
s'écrivent, en négligeant les mouvements verticaux
et en faisant certaines approximations :
-
Résoudre le
système d'équations différentielles précédent
par la méthode complexe en posant
, sachant qu’initialement
.
-
En déduire
la durée d'un tour complet du plan
d’oscillation de ce système.
Application numérique pour
λ =
0°, λ =
43°35' et λ =
90°.
M10.5. Pendule de Foucault.
Corrigé.
1. Equation vectorielle du mouvement.
On
étudie le mouvement de masselotte A dans le
référentiel terrestre (R) non galiléen qui
est soumise à :
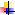son poids
(la force d’inertie d’entraînement due au caractère
non galiléen du référentiel terrestre est incluse
dans le poids de la masselotte A, cependant
on ne tient pas compte de l’effet de cette force sur
la direction du poids, seul est pris en compte la
différence entre la valeur du champ de pesanteur et
celle du champ de gravitation)
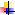la tension
du fil
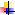la force d’inertie de Coriolis
où
est la vitesse de la masse dans le référentiel
terrestre.
La
relation de la dynamique s’écrit :
2. Equations différentielles du mouvement.
On
effectue la projection de l’équation vectorielle du
mouvement dans la base du référentiel terrestre :
Si
l’on néglige les mouvements verticaux on a :
D’autre part :
On
obtient alors d’après (3) que
Dans l’équation (1) le terme
est alors peu différent de
Les
équations (1) et (2) peuvent alors s’écrire :
En
posant
on aboutit aux équations proposées dans l’énoncé :
On
peut remarquer qu’à l’équateur on a
et que l’effet de la force de Coriolis est nulle
compte tenu des approximations effectuées.
3. Résolution des équations différentielles.
Pour ce système d’équations différentielles couplées
on utilise la méthode de la variable complexe en
posant :
En
effectuant l’opération (4) + j(5) on
obtient :
Soit en fonction de la variable complexe :
On
recherche des solutions de la forme
avec r complexe ce qui conduit à l’équation
caractéristique :
Le
discriminant réduit à pour expression :
Les
solutions sont :
Comme
les solutions de l’équation caractéristique peuvent
s’écrire :
La
variable complexe s’écrit alors :
Pour calculer les deux constantes d’intégration on
calcule dans un premier temps la dérivée temporelle
de la variable complexe :
Comme à la date t = 0 on a :
On
obtient ainsi :
Et
finalement :
Le
développement de la variable complexe
permet d’obtenir par identification les expressions
de x et de y :
4. Calcul d’un tour complet suivant la latitude.
Le
terme
qui est présent dans l’expression de la variable
complexe représente une rotation du plan
d’oscillation du pendule autour de l’axe vertical
Oz avec une vitesse angulaire
.
La
période T de rotation de ce plan s’écrit :
