EM7.3. Détermination d’une distribution de courants.

Enoncé.

Soit l’espace pour lequel on a (en coordonnées cylindriques) :

 pour r < a et

 pour r >a avec k une constante.

On demande de déterminer les caractéristiques de la distribution de courants qui engendre ce champ magnétique.

 

 

 

 

E7.3. Détermination d’une distribution de courants.

Corrigé.

Le vecteur densité de courants est a priori de la forme :

             

Comme le champ magnétique est invariant par rotation autour de l’axe Oz et par translation le long de même axe, la distribution de courants ne dépend pas alors des variables  et z.

             

Comme le champ magnétique « tourbillonne » autour de ses sources et qu’il est dans ce problème orthoradial on doit alors avoir :

             

On peut montrer cela en utilisant deux contours d’Ampère élémentaires particuliers :

Contour  : Contour fermé KLMN compris entre z et z + dz avec r contant :

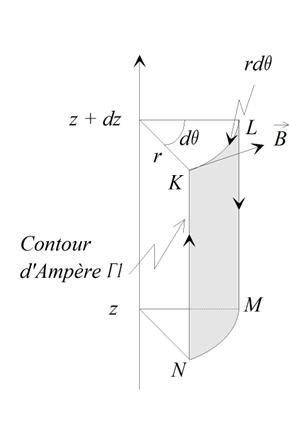
L’application du théorème d’Ampère sur ce contour donne :

             

On obtient :

             

Contour  : Contour fermé rectangulaire contenu dans un plan  K’L’M’N’ compris entre z et

z + dz et r et r + dr :

 

Le théorème d’Ampère s’écrit sur ce nouveau contour fermé :

 

On obtient ainsi :

             

 

Pour déterminer la troisième composante du vecteur densité de courants on utilise de nouveau le théorème sur un contour  comme l’illustre la figure suivante :

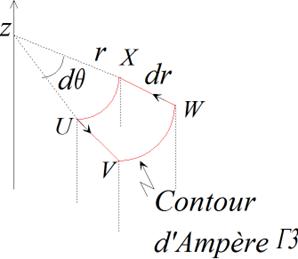
De nouveau le théorème d’Ampère s’écrit sur ce contour fermé :

 

Pour r < a       car  

Pour r > a       car k = constante

Ces trois résultats permettent d’affirmer qu’il n’existe pas de courant volumique.

Le champ magnétique subit une discontinuité de sa composante tangentielle en r = a. Les courants sont donc répartis sur la surface cylindrique de rayon r = a.

La discontinuité du champ s’écrit :

             avec  vecteur normal à la distribution surfacique de courant au point

            considéré .

Dans le cadre de l’exercice on a :

             

En multipliant vectoriellement par le vecteur  on obtient :

             

On peut alors conclure que la distribution surfacique de courants qui engendre ce champ magnétique dans l’espace a pour expression :

 et est située en r = a