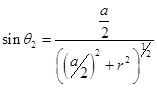EM6.1. Champ
magnétique créé par une spire carrée.
Enoncé.
On
considère une spire carrée, de côté a, placée
dans le plan Oxy et parcourue par un courant
d’intensité I constant.
1.
Montrer que le champ magnétique en un point
M de l’axe a pour expression :
2.
Déduire du calcul précédent le champ
magnétique créé par une spire polygonale régulière
de N côtés.
EM6.1. Champ
magnétique créé par une spire carrée.
Corrigé.
1. Champ magnétique en point M de l’axe.
Le
champ magnétique sur l’axe Oz d’une spire
carrée
de
côté a, placée dans le plan xOy est la
somme vectorielle des champs
crées
par chaque segment :
On
recherche dans un premier temps le champ magnétique
créé par un segment de longueur a, en un
point M de sa médiatrice. On note H le
projeté de M sur le segment,
et
.
Pour effectuer ce calcul de l’intégrale, on
introduit le paramètre angulaire
pour
exprimer les variables z et PM et en
remarquant que
.
On
en déduit :
Comme
,
et
que
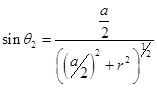on
obtient :
En
M, les composantes perpendiculaires à l’axe
Oz se compensent deux à deux entre segments
se faisant face. Par conséquent :
Comme
et
que
le
champ magnétique s’exprime alors sous la forme :
2. Cas d’une spire polygonale.
Le
calcul précédent se généralise au cas d’un polygone
régulier de N côtés. Le champ magnétique a
pour expression :
où
ont
les mêmes significations que précédemment.
