E4.7. Impédance itérative.

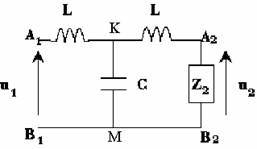
Le circuit représenté ci-dessous est alimenté entre les bornes d'entrée A1 et B1 par un générateur de tension sinusoïdale de pulsation ω réglable, d’impédance interne négligeable qui fournit une tension u1  de valeur efficace U1 constante.

Les inductances sont pures et le condensateur est parfait.

On donne : L = 2.10-3 H  ; C = 1,0.10-9 F.

 

1.    Exprimer en fonction de ω, L, C et de , impédance  branchée à la sortie, l'impédance d'entrée , vue des points A1 et B1.

2.    Déduire de ce calcul l'impédance caractéristique , définie par la condition  =  = .

3.    Pour quelles valeurs de la pulsation ω l’impédance caractéristique est-elle modélisable par un résistor de résistance Rc ?

       On branche à la sortie entre les bornes A2 et B2 un résistor de résistance Rco égale à la valeur de Rc lorsque la pulsation ω tend vers zéro. Montrer que : Rco = .