E2.17. Transformation triangle-étoile. Théorème de Kennely.
Enoncé.                                             

On considère les circuits électriques de la figure suivante :

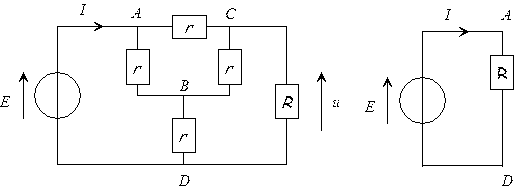
1. En appliquant le théorème de Kennely, déterminer la résistance R pour que l'intensité I soit la même dans les deux cas.
2. Que vaut alors u/E ?
3. Si R vérifie la condition précédente, déterminer le rapport u/E si on intercale n fois l’ensemble des quatre résistances r.

 

Théorème de Kennely : En un nœud N d’une association en triangle, la résistance équivalente d’un montage en étoile est :  

 

www.kholaweb.com

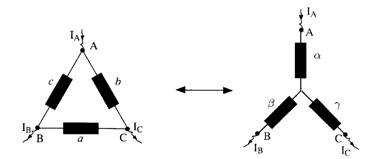
E2.17. Transformation triangle-étoile. Théorème de Kennely.
Corrigé.

1. Expression de la résistance R.

La portion de circuit ABCA est disposée en « triangle ». On la transforme en « étoile » en utilisant le théorème de Kennely et on utilise les notations de l’énoncé.

             

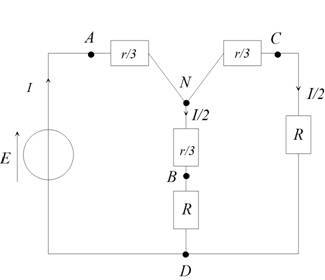
Les branches NBD et NCD sont en dérivation. La résistance équivalente  à la portion de circuit comprise entre les points N et D a pour expression :

             

La résistance équivalente à la portion de circuit comprise entre les points A et D que l’on note  est égale à :

             

On veut que  d’où :

             

Il reste :

             

On obtient ainsi :

             

2. Expression de u/E.

Comme R = r, les branches NBD et NCD sont identiques,  le courant dans les différentes branches vérifie alors :

             

Comme  et que  on obtient :

             

3. Cas où le motif est intercalé n fois.

Le réseau considéré est maintenant le suivant :

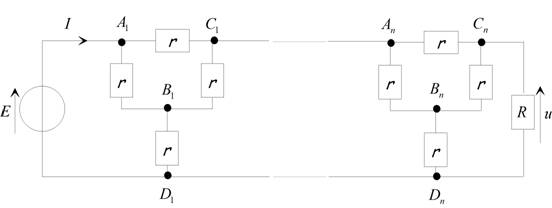
L’application du théorème de Kennely permet alors de le représenter sous la forme suivante avec la condition R = r :

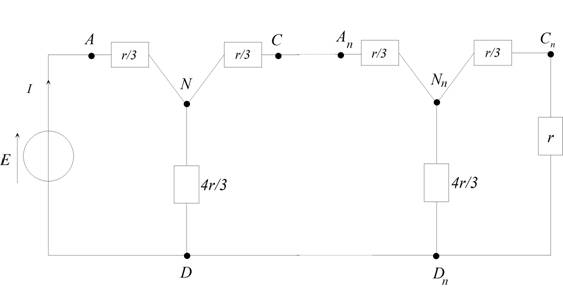
Si l’on part de la droite, le dipôle équivalent à l’association comprise entre les points  et D_n a une résistance équivalente à r d’après le calcul effectué à la question 1. On retrouve ainsi la même association entre les points A_n-1 et D_n-1 et cela ainsi de suite jusqu’au générateur.

L’association est ainsi équivalente à un générateur de f.é.m E branché sur un résistor de résistance r et débitant un courant .

En partant maintenant de la gauche, le courant se divise en deux au premier nœud N₁ en  dans les branches N₁D₁ et N₁C₁ qui sont identiques car . Il en va de même au nœud N₂ où il se divise de nouveau en deux avec la valeur .

On peut ainsi dire que le courant  qui arrive au nœud N_n se divise en  qui circule alors dans la résistance R = r.

La tension u a alors comme expression :