T6.6. Détente de
Joule-Kelvin d’un fréon dans une machine
frigorifique.
1. Diagramme de Clapeyron.
Allure du diagramme :
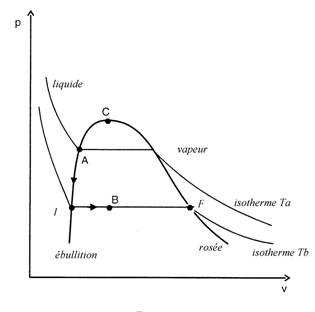
Le point I correspond à l’apparition de la
première bulle de vapeur lors d’une évolution sur
cette isotherme de la gauche vers la droite. Le lieu
de ces points I lorsque la température varie
est appelé la courbe d’ébullition.
Le point F correspond à
la disparition de la dernière goutte de liquide lors
d’une évolution sur cette isotherme de la gauche
vers la droite, ou à l’apparition de la première
goutte de liquide lors d’une évolution dans le sens
contraire, le lieu des points F lorsque
la température varie est appelé la courbe de
rosée.
La réunion de la courbe de
rosée et de la courbe d’ébullition est la courbe
de saturation qui limite l’existence d’une
vapeur saturante.
Remarque importante : On
ne peut faire figurer dans ce diagramme l’évolution
conduisant de A à B car les états
intermédiaires ne sont pas des états d’équilibre
thermodynamique et sont donc non connus car
l’évolution n’est ni mécaniquement et thermiquement
réversible.
2. Points A et B.
On suppose que la pression
indiquée pour le point A est la pression de
vapeur saturation et comme
, le point A fait partie de la courbe
d‘ébullition.
Compte tenu du chapitre (!) et
de la question suivante, on peut supposer un
équilibre diphasé pour lequel on a donc :
. Le point B est situé sur l’isotherme
entre les points I et F.
3. Détermination de x
vapeur au point B.
L’évolution AB est une
détente de Joule-Kelvin donc isenthalpique. On
exprime le caractère particulier de cette
transformation en déterminant
.
Comme l’enthalpie est une
fonction d’état, sa variation entre les états A
et B ne dépend pas du chemin suivi entre ces
deux états. On considère alors le chemin particulier
AIB où AI est une évolution le long de
la courbe d’ébullition sur laquelle on suppose le
fréon dans l’état liquide et IB une évolution
isotherme à la température
et isobare à la pression
(transformations mécaniquement réversibles).
On a alors :
4. Variations d’entropie.
On utilise le même chemin pour
effectuer la détermination de cette variation
d’entropie :
