M3.1. Equilibre d'une charge sur un plan incliné.

 

1. Energie du système.

 

On pose l’énergie potentielle de pesanteur nulle dans le plan horizontal contenant la particule A et l’énergie potentielle électrique nulle lorsque les particules se trouvent à l’infini l’une de l’autre.
En considérant un axe des cotes orienté verticalement vers le haut on a :

Ep_pesanteur = Ep_p = mgh

Pour l’énergie potentielle électrostatique, on a en notant x la distance séparant les deux charges et en prenant le zéro de l’énergie potentielle lorsque les charges sont l’infini l’une de l’autre :

 

L’énergie mécanique du système s’écrit :

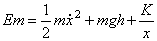
On exprime la hauteur de la particule B en fonction de x :

h=xsinα

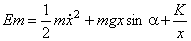
2. Position d’équilibre.

 

La position d’équilibre x_e correspond à un extremum du potentiel de la particule B.

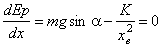
Soit :

 

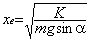
3. Equation du mouvement.

Le système des deux charges en interaction est supposé conservatif. L’énergie mécanique est donc constante au cours du temps. D’où :

 

 

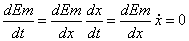
Dans le cas où l’objet B est en mouvement on a :

 

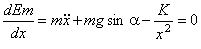
On pose :

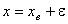 où ε << x_e

On injecte cette expression dans l’équation différentielle :

En exprimant xe, on obtient :

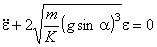
La solution de cette équation est de la forme :

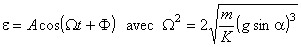
La particule B oscille autour de la position x_e. Cette position d’équilibre est donc stable.