E6.4. Filtre à structure de Rauch.
Enoncé.
On
considère le montage suivant où l’A.O. supposé idéal
fonctionne en régime linéaire. La tension d’entrée
ve(t) est sinusoïdale, de
pulsation ω.
1.
Chercher sans calculs la nature du filtre.
2.
Déterminer la fonction de transfert en
fonction de
avec
.
3.
Tracer le diagramme de Bode
E6.4. Filtre à structure de Rauch.
Corrigé.
1. Nature du filtre.
En basse fréquence, les condensateurs se comportent
comme des interrupteurs ouverts. On a le montage
équivalent suivant :
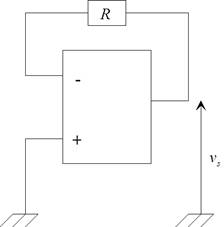
La tension
est nulle car aucun courant ne peut circuler
dans la boucle de rétroaction dans le cas d’un A.O.
idéal.
En haute fréquence la situation est plus délicate à
étudier car si l’on remplace les condensateurs par
des interrupteurs fermés on a alors un montage
équivalent qui conduit à une contradiction :
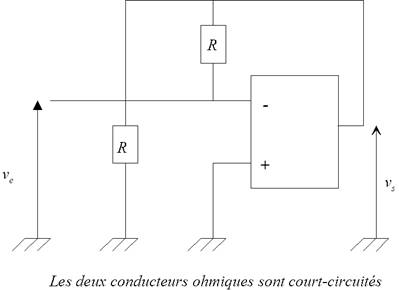
La tension de sortie serait alors égale à :
or
Cependant, en considérant qu’en haute fréquence les
condensateurs sont de très bons conducteurs,
l’intensité du courant se répartit alors de la
manière suivante (>) :
Le courant passe alors principalement par les
branches EA et AHM car présentant une
impédance bien plus faible que les branches AM
et ABH.
On a dans cette configuration :
et
.
Comme les branches EA et AH sont
identiques et en série on a alors :
.
Il s’ensuit qu’aucun ne circule dans la branche
EAH et qu’en haute fréquence le montage se
comporte comme un dispositif inverseur.
Ce
dispositif a le comportement de filtre passe-haut.
2. Fonction de transfert.
On applique le
théorème de Millman aux points A et - :
En
A :
A l’entrée inverseuse
de l’A.O. :
En remplaçant dans (1) cette dernière expression du
potentiel complexe au point A on obtient :
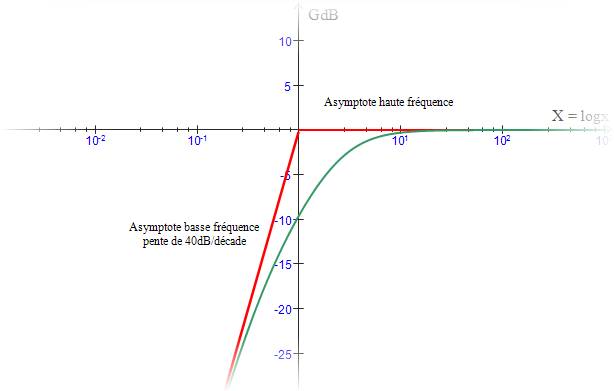
3. Diagramme de Bode.
Réponse en gain :
Par définition du gain on a :
Le filtre a le comportement asymptotique suivant :
Pour la valeur particulière x = 1 :
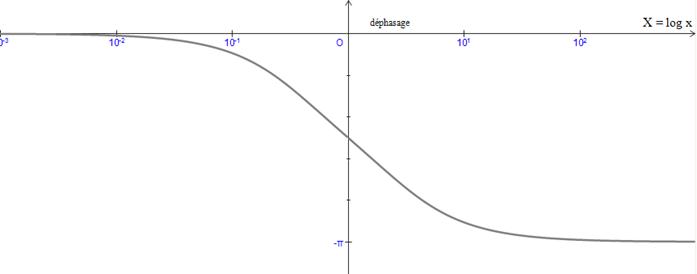
Réponse en phase :
·
Pour x <1 :
·
Pour x >1 :
Pour :
