E3.5. Etude d'un circuit (RL, R//C) en régime transitoire.
On applique la loi des mailles :
(a) 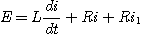
(b) 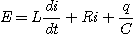
La dérivation de l'équation par rapport au temps permet d'obtenir
l'expression de l'intensité i1
:
(c) 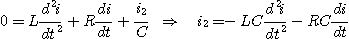
En appliquant la loi des noeuds et en injectant le résultat de (c) dans (a),
on détermine l'expression de i :
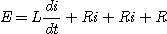
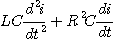
On divise par R :
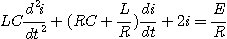
Or :
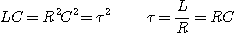
On obtient l'équation différentielle suivante :
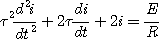
Le discriminant de l'équation caractéristique de l'équation différentielle
sans second membre est négatif :
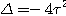
Les racines de l'équation caractéristique sont :
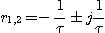
La solution particulière de l'équation différentielle avec second membre est
:
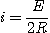
La solution générale de l'équation différentielle avec second membre est :
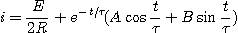
Les conditions initiales permettent de déterminer les deux constantes
d'intégration A et B :
A t = 0 :
i = 0 La continuité du courant est assurée par la bobine.
q = 0 et i = 0
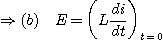
On obtient :
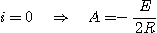
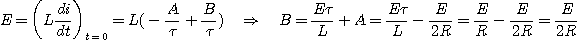
L'équation vérifiée par i est :